Stochastic Streets Riddler
In this post, I describe my (lazy) solution to FiveThirtyEight’s most recent Riddler Problem. This problem asks us to imagine living in a city which has a square gridded network of one-way streets whose orientations were assigned completely at random. Supposing that you live in the upper left corner of the city and work in the lower right corner, we’re asked: How likely is it that you can navigate from your home to work via the city’s street network?
The original prompt asked us to consider a square city two blocks across by two blocks high, however I chose to approach the problem more generally, considering square cities with an arbitrary width. As usual for these sorts of problems, I approached the problem from two directions, coming up with an exact analytical solution, and then estimating the result by simulation.
Unfortunately, I couldn’t think of an elegant exact solution… so I resorted to a brute force approach, simply enumerating all possible city layouts and counting the fraction with a navigable path from home to work. The brute force nature of my exact approach meant that I could only consider relatively small cities. In fact, letting \(n\) denote the number of intersections across the city (i.e. one more than the number of city blocks!), I was only able to “solve” the problem for \(n = 2,3,4\). But, because this range included the \(n = 3\) case discussed in the prompt, I decided to call it quits for exact methods after that 🙂
More interestingly, for cities of size \(n = 2, \ldots, 20\), I estimated the probability that you could navigate by simulating random street assignments and counting the fraction that had a navigable path from home to work. In principle, this approach would have worked for any city size, but I figured \(20\) was big enough.
As usual, I’ve made the script for my solution available, and you download the solution script (in Julia) here. This time, I wrote my solution as a Pluto notebook, which I’ve rendered statically for viewing here.
Simulation Solution
To begin with, lets take a look at a couple realizations of random street
assignments for the \(2 \times 2\) block / \(n = 3\) case. In the first example,
there is no path from home (labeled \(1\)) to work (labeled \(9\)). In the
second example, you can get to work using the path 1 => 2 => 5 => 8 => 9 or
1 => 2 => 5 => 6 => 9. Unfortunately, although you can get to work in this city,
there isn’t any way for you to get back home!
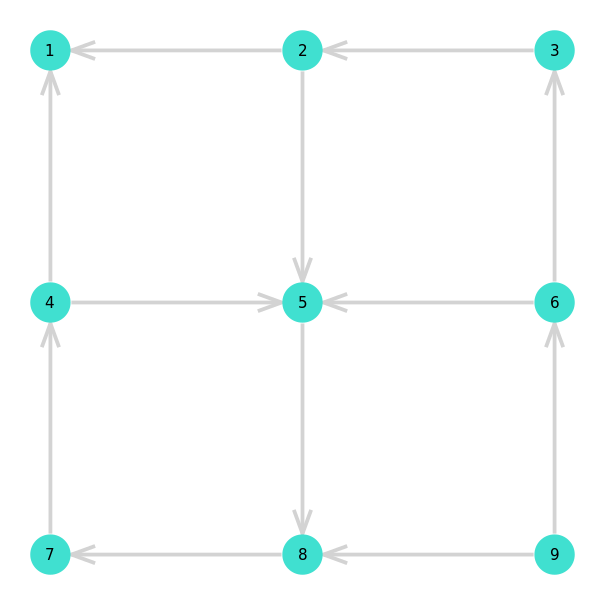
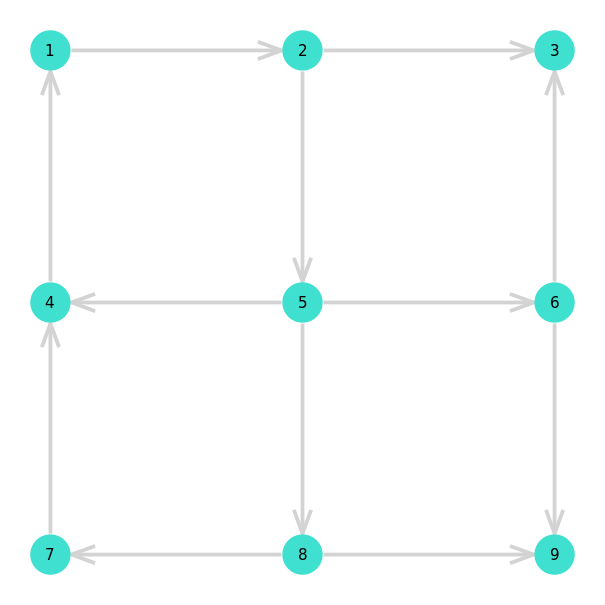
For each random street assignment, I determined whether there was a path from
home to work by constructing a directed graph from the street assignment using
LightGraphs.jl. From there, I
determined whether the network had a path from home to work using the very aptly
named has_path function.
For each city size \(n = 2, 3, \ldots, 20\), I generated one million random street assignments and determined the fraction which had a navigable path from home to work. The results are summarized in the following figure.
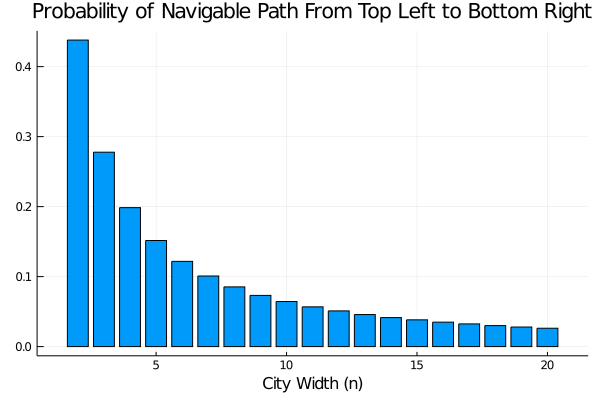
The following table summarizes the results for small \(n\), and the complete data set can be downloaded here.
| City Width | Probability Navigable |
| 2 | 0.437949 |
| 3 | 0.277747 |
| 4 | 0.198520 |
So, we see that the solution for \(n = 3\) is around \(27.7\%\).
(Lazy) Exact Solution for Small Cities
As I mentioned in the introduction, I couldn’t think of a good analytical solution to this problem, so I decided to implement a bad solution - i.e. I just brute forced the answer. If the problem had asked for a slightly larger city, say a \(4 \times 4\) grid (i.e. \(n = 5\)) then this approach would not have been feasible. However, for cities of size \(n = 2,3,4\) there are only \(2^4, 2^{12}\), and \(2^{24} = 16,777,216\) street layouts respectively1, so these can all be easily brute-forced.
To perform the computation, I followed largely the same steps that I discussed in the previous section. The only difference here, was that I looped over all possible street layouts instead of generating them at random.
The following table shows the results:
| City Size | Probability Navigable |
| 2 | \(7 / 16 \approx 0.4375\) |
| 3 | \(1,135 / 4,096 \approx 0.2771\) |
| 4 | \(3,329,245 / 16,777,216 \approx 0.1984\) |
From the table, we see that for a \(2\times2\) city (i.e. \(n = 3\)) there’s about a \(27.7\%\) chance that we’ll be able to drive to work!
Footnotes
-
To see this, first draw out the cities and convince yourself that cities of these sizes respectively have a total of \(4, 12\) and \(24\) streets. From there, note that, because each street can be in one of two directions there are \(2^{n_\text{streets}}\) possible layouts for any city. ↩