McFar Points
A few weeks back, a friend asked me if I was familiar with the concept of the “McFarthest Spot.” I wasn’t familiar with the idea, but a quick search informed me that it is the point in the continental United States where you are further away from a McDonald’s than at any other point. The concept seems to have first been considered by Stephen Von Worley as discussed in this post, and tends to randomly resurface on the internet from time to time, especially when the McFarthest Spot changes.
After a few minutes of thinking about it, I realized that I wouldn’t be satisfied with knowing that someone else had computed the location of the McFarthest Spot, but that I would have to try to compute it for myself. So, that’s what I will be discussing in this post. As usual, I wanted to “show my work,” so I have made the notebooks that I generated this post with available in this repository.
Ultimately, I wasn’t actually able to compute the “true” McFarthest Spot, because I didn’t obtain a comprehensive list of McDonald’s restaurants in the lower 48 states. It seems that fast-food chains aren’t exactly forth-coming with complete lists of all of their locations. While I’m not entirely clear on why this kind of information can’t be easily found on the internet, it seems that there must be some kind of value in this sort of data, since I found a lot of data-scraping sites offering to sell it to me for around $100. Since I didn’t really want to pony up $100, and didn’t feel like scraping it myself, I settled on an alternate solution: I just grabbed the location data from OpenStreetMap (through the Overpass API). Unfortunately, it seems that OpenStreetMap is missing most of the United States’ McDonald’s, since I was only able to find around 3,400 McDonald’s in the continental US when there should be around 13,000. (On the other hand, my Overpass query could be incomplete). Despite my dataset’s incompleteness, the McFarthest point that I found was pretty close to the “true” McFarthest Spot. On the other hand, my McFarthest point is slightly further away from a neighboring McDonald’s than the “true” McFarthest spot.
Throughout this post, I’ll use the term “McFarthest point” as a short-hand for “the point in a region furthest away from a given fast food chain.” In addition to computing the McFarthest Point for McDonald’s in the lower 48, I also computed McFarthest points within each state (also D.C.), and I found similar points for Burger King and Wendy’s.
How Can You Compute McFarthest Points?
Before getting to the McFarthest Points themselves, I’d like to give a bit of detail on how you (or rather I) would go about computing a McFarthest Point. One way to do this is to first compute a Voronoi diagram for the region of interest. A Voronoi diagram for a discrete set \(S\) is a collection of regions \(R_s\) for each point \(s \in S\), where every \(x \in R_s\) is closer to \(s\) than any other point in \(S\). The regions \(R_s\) are collectively referred to as Voronoi cells, and each point \(s\) is referred to as a generator for its Voronoi cell. When distances are reckoned using the Euclidean distance, the Voronoi cells are polygons, but the sides may curve when a different distance is used (which we will do).
Once you have your Voronoi diagram, you can compute the global McFarthest Point by computing local McFarthest Points within each Voronoi cell and then simply identifying the cell \(R_s\) whose local McFarthest Point is furthest away from its generator point \(s\). To compute the local McFarthest points, it’s not hard to convince yourself that within each cell \(R_s\) the greatest distance from \(s\) must be achieved on the boundary of \(R_s\). In fact, the maximum distance must be achieved at one of the boundary vertices. As a result, to compute the McFarthest point you only need to find the vertex \(v\) that maximizes the finite set:
\[\{ d(v, s) : v \in \text{Vertices}(R_s), s \in S \}\]So an algorithm for computing McFarthest points looks like:
- Compute the Voronoi diagram for \(S\).
- Compute distances \(d(v, s)\) for all \(v \in R_s\) and all \(s\in S\).
- Find \(v,s\) for which \(d(v,s)\) is largest. \(v\) is the McFarthest point, and \(d(v,s)\) is the max distance.
As a practical aside, all distance computations need to be done using the same distance function. Specifically, you need to construct the Voronoi cells using \(d\), and not some other distance \(d'\). Because I used Scipy for my Voronoi diagram computations, and because the Earth is essentially a sphere, this essentially forced me to use Scipy’s Spherical Voronoi diagram functions.
McFarthest Points
The following images show the nationwide and statewide McFarthest points that I found for McDonald’s, Burger King, and Wendy’s using OpenStreetMap data. In these figures, I have also plotted the store locations and the Voronoi cell boundaries.
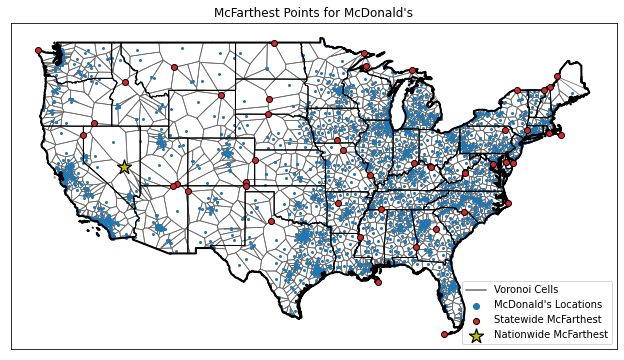
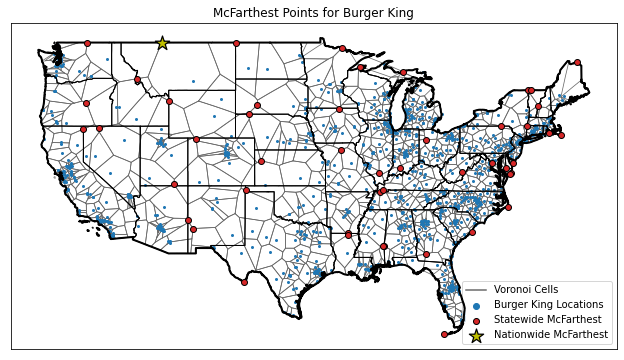
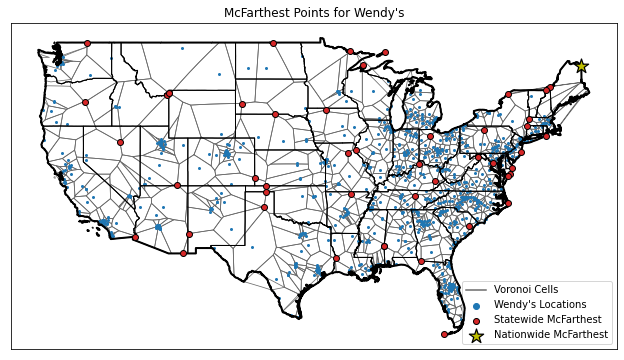
For the most part, it seems that if you want to get far away from fast food, you’re going to want to go out North-West near Canada. Or maybe it’s just that OpenStreetMap has less coverage in those areas? Either way, here’s a summary table of McFarthest points I found:
| Chain | Distance (miles) |
McFarthest Point (lat, lon) |
Nearest Store (lat, lon) |
|---|---|---|---|
| McDonald’s | 154.10 | (38.60, -115.77) | (36.80, -114.10) |
| Burger King | 280.45 | (49.00, -111.79) | (47.63, -117.54) |
| Wendy’s | 312.32 | (47.07, -67.79) | (44.50, -73.12) |
Datasets for all locations and all nationwide / statewide McFarthest points are available below.
McFarthest Point Stability
The true McFarthest point currently sits in Nevada, but it used to sit all the way up in South Dakota. This dramatic shift evidently stems from the closure of a single McDonald’s store, so it’s a bit surprising that I was able to more or less match the true McFarthest point with my very incomplete data. The computation of the McFarthest point is fairly sensitive to the data that you use to compute it!
To illustrate this sensitivity, I recomputed the nationwide McFarthest point with incomplete datasets of progressively increasing size, ranging from 3 to 3396 McDonald’s locations. The results are plotted in the following animation.
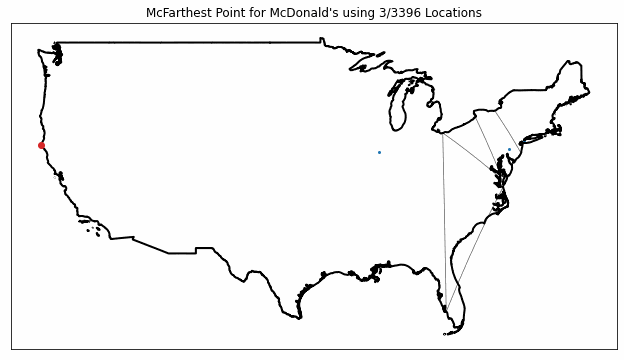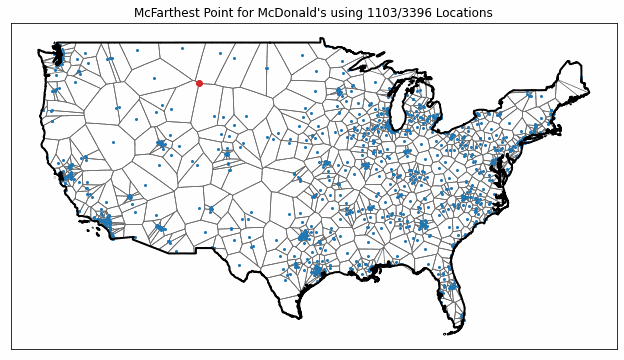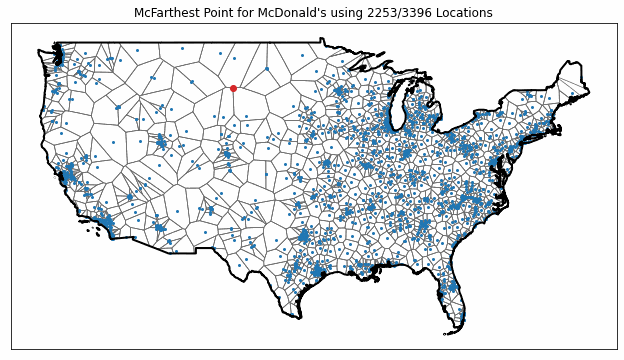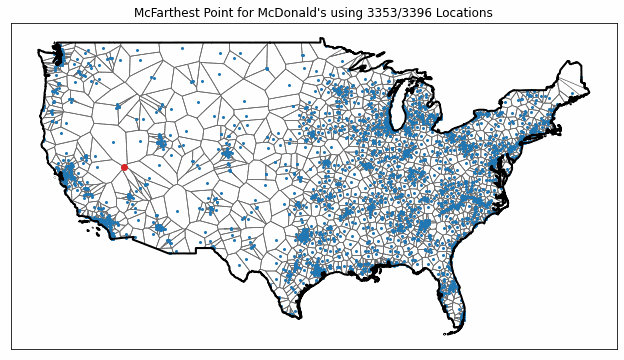
As you can see from the figure, the McFarthest point (plotted in red) jumps around quite a bit as more data is included, showing how just a few stores can have a huge impact on the results.
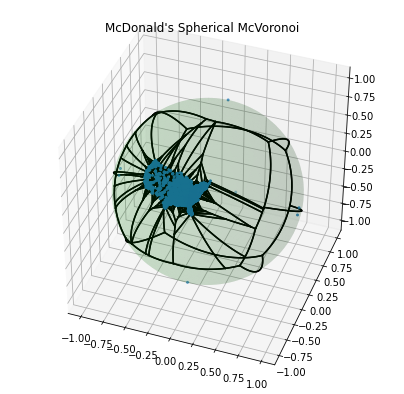
Spherical McVoronoi McDiagram
As a final aside, I wanted to give a sense of the spherical Voronoi diagrams that I used in their original context - as opposed to projecting them into the plane. The following figure shows the spherical Voronoi diagram for McDonald’s. A few extra points have been added around the globe to help constrain my diagram to the western hemisphere.
Downloads
| Locations in Lower 48 | McFarthest Points |
|---|---|
| BurgerKing_Locations.csv | BurgerKing_McFarthest.csv |
| McDonalds_Locations.csv | McDonalds_McFarthest.csv |
| Wendys_Locations.csv | Wendys_McFarthest.csv |
Data represent locations found in OpenStreetMap data as of Oct, 21 2020.
Edits
2020-10-21: An earlier version of this post was unable to match the “true” McFarthest Spot, due evidently to incomplete data. Previously, I sourced data from a local installation of Overpass, however, I recomputed everything today using data sourced from the overpass-api.de. To my great surprise, my computation is now much more in-line with the location of the the “true” McFarthest spot 🙂